Skip to contents

2. Estimate

Source: vignettes/2-estimate.Rmd
2-estimate.Rmd

Introduction

Estimating the the models described in Explaining Recruitment to Violent Extremism: A Bayesian Case-Control Approach (ERVE) requires just two steps:

  1. Prepare the data sources in list format using data.prep()
  2. Estimate the model using fit()

This explainer vignette walks you through the second of these two steps.

Setup

First install the package from source if not already installed.

devtools::install_github("extremerpkg/extremeR")

We then load the package into memory as follows. We will also be using several functions from the rstan package.

Load data

Then we load the pre-formatted data into memory as follows.

data(data.list)

Estimate model

And we are then ready to estimate the ERVE model for the Egyptian case-control data.

The fit() function has a series of parameters that we tabulate and describe below.

Argument Description
data list, survey and shapefile combined list object created with the data.prep() function
show_code logical, should the stan code print on the screen at the end of the run? Defaults to TRUE
contamination logical, should the model include the Rota et al. (2013) style contamination layer? Defaults to TRUE
offset logical, should the model include a King and Zeng (2001) style offset ? if contamination is also specified, this will be a contaminated-offset. Defaults to TRUE
beta_prior string, what prior should the regression coefficients have? Choice between: “normal” and “cauchy”
small_area_prior string, what should be the small-area effects type? Choice between: “fixed,” “random,” “ICAR,” and “BYM2.” Specify NA for no area effects. Defaults to “fixed”
large_area_prior string, what should be the large-area effects type? Choice between: “fixed” and “random.” Specify NA for no area effects. Defaults to NA.
intercept_scale integer, scale of intercept; arguments taken from rstan, see here for further information
iter integer, number of draws; arguments taken from rstan, see here for further information
warmup integer, number of warmup draws; arguments taken from rstan, see here for further information
thin integer, number to thin draws; arguments taken from rstan, see here for further information
cores integer, number of cores to use; arguments taken from rstan, see here for further information
chains integer, number of chains; arguments taken from rstan, see here for further information
control list, tree depth and adapt delta; arguments taken from rstan, see here for further information
verbose logical, print full stan output? Defaults to TRUE 
fit_object = fit(
  data = data.list,
  show_code = T,
  contamination = T,
  offset = T,
  beta_prior = "cauchy",
  small_area_prior = "BYM2",
  intercept_scale = 10,
  large_area_prior = "random",
  iter = 25000,
  warmup = 22500,
  thin = 4,
  cores = 4,
  chains = 4,
  control = list(max_treedepth = 25, adapt_delta = 0.99),
  verbose = T
)

Check MCMC convergence

We can then check the summary convergence statistics by using the monitor() function in rstan.

mon_egypt <- rstan::monitor(rstan::extract(fit_object, permuted = FALSE, inc_warmup = TRUE))

And we could inspect the output for, e.g., the \(\hat{R}\) values as follows.

rhats <- mon_egypt$Rhat
plot(rhats)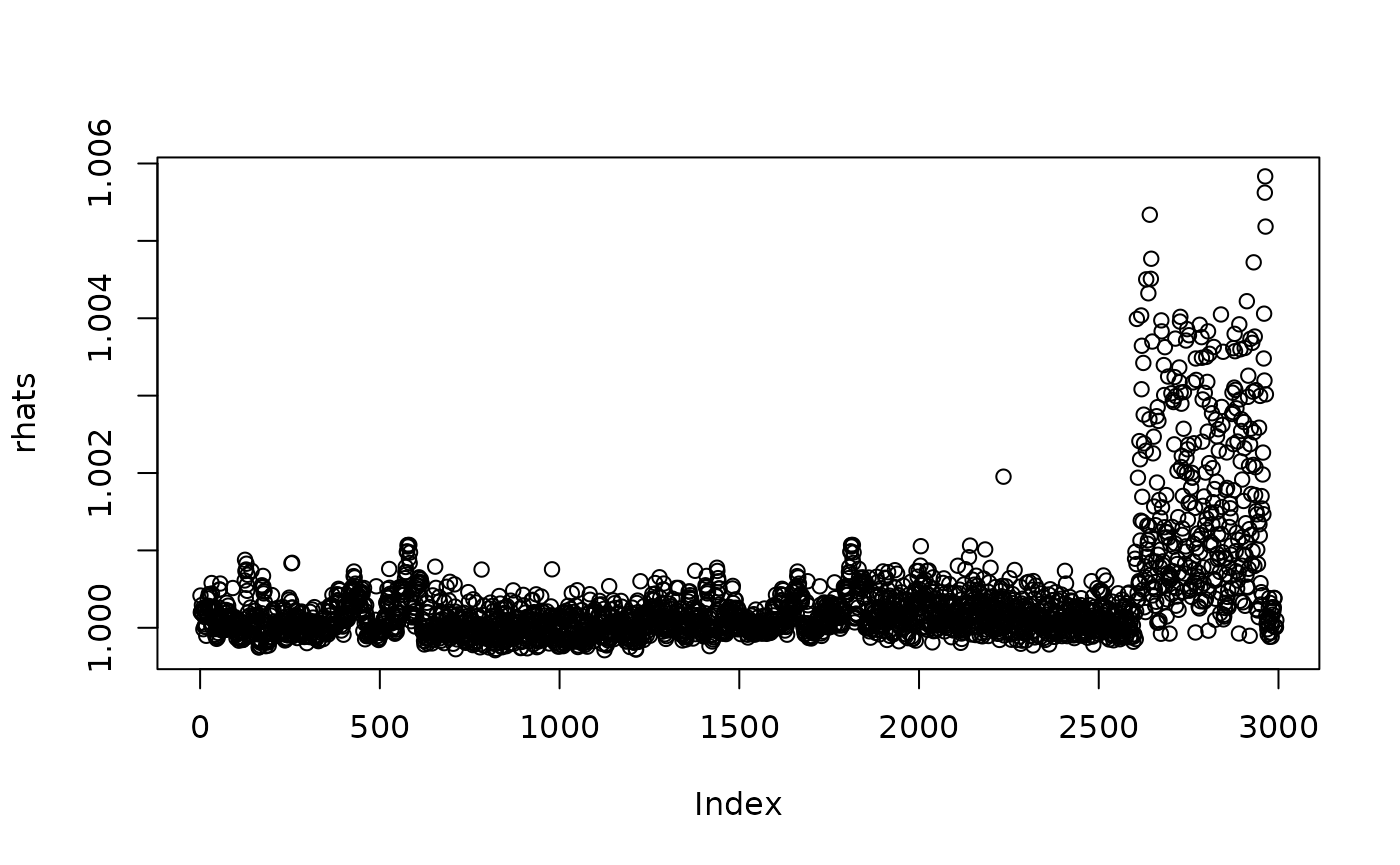

Inspect output

And we are able to access the estimated parameters of the “stanfit” object by using the extract() function in rstan.

betas_egypt <- rstan::extract(fit_object ,
                           pars = c('beta'),
                           permuted = TRUE,
                           inc_warmup = FALSE,
                           include = TRUE)

Or printing from the fit object directly.

print(fit_object, pars=c("beta"), probs=c(.1,.5,.9))
## Inference for Stan model: anon_model.
## 4 chains, each with iter=25000; warmup=22500; thin=4; 
## post-warmup draws per chain=625, total post-warmup draws=2500.
## 
##            mean se_mean   sd    10%    50%    90% n_eff Rhat
## beta[1]  -13.26    0.02 0.88 -14.41 -13.19 -12.20  2265    1
## beta[2]    0.56    0.01 0.27   0.22   0.55   0.91  2683    1
## beta[3]   -0.38    0.02 1.05  -1.65  -0.39   0.84  2513    1
## beta[4]    0.05    0.01 0.31  -0.35   0.06   0.45  2361    1
## beta[5]    0.18    0.00 0.23  -0.11   0.18   0.47  2462    1
## beta[6]   -0.85    0.01 0.47  -1.46  -0.81  -0.30  2470    1
## beta[7]    1.36    0.01 0.73   0.49   1.27   2.31  2472    1
## beta[8]   -0.15    0.01 0.57  -0.87  -0.15   0.57  2004    1
## beta[9]   -0.29    0.01 0.61  -1.05  -0.27   0.43  1698    1
## beta[10]   0.29    0.01 0.60  -0.44   0.27   1.04  2193    1
## beta[11]  -0.84    0.02 0.86  -1.96  -0.74   0.16  2318    1
## beta[12]  -0.09    0.02 0.72  -0.99  -0.06   0.77  1873    1
## beta[13]   1.59    0.02 0.73   0.68   1.57   2.54  1674    1
## beta[14]  -0.26    0.01 0.64  -1.09  -0.23   0.49  2173    1
## beta[15]  -0.39    0.01 0.60  -1.21  -0.34   0.33  2208    1
## beta[16]  -1.15    0.03 1.26  -2.75  -0.99   0.24  2457    1
## beta[17]   0.48    0.00 0.26   0.17   0.47   0.82  2674    1
## 
## Samples were drawn using NUTS(diag_e) at Tue Mar  1 23:48:57 2022.
## For each parameter, n_eff is a crude measure of effective sample size,
## and Rhat is the potential scale reduction factor on split chains (at 
## convergence, Rhat=1).